在探究中发展理性思维
(省教育学会三等奖)
无锡外国语学校 王超
在教学过程中,经常遇到这样一些学生,讲过的题目改变一些条件,或图形旋转一个角度,又不会做了。有的老师认为学生没有认真学,我认为是没“学到位”——他们的学习只停留在表面,感性上,而没有上升到理性思维。
物理学家劳厄曾经说过,对于科学教育重要的不是获得知识,而是发展思维能力。教育给予人们的无非是一切学过的东西都遗忘掉的时候所剩下来的东西。“剩下来的东西”是什么?——理性思维。探究性学习虽然只是初中数学教育的一部分,但蕴含着许多理性思维的教学要素,实施探究性学习的方式,从根本上讲就是在实施有效课堂教学,促进学生理性思维的发展。
数学是研究现实世界中数量关系和空间形式的科学。简单地说,是研究数和形的科学。是一门发散人的思维的学科。数学学习是一个特殊的认识过程,它当然要受制于一般的认识规律。但是数学学习的对象有其自身的特点(如抽象性、概括性较高、知识的前因后果联系比较紧密等)。这样,数学学习又有其特殊性——较强的理性思维。因此,要想学好数学,必须有较强的理性思维。
理性思维是一种有明确的思维方向,有充分的思维依据,能对事物或问题进行观察、比较、分析、综合、抽象与概括的一种思维。说得简单些理性思维就是一种建立在证据和逻辑推理基础上的思维方式。数学是一门逐步建立学生理性的思维方式的课程,对理性思维的培养应成为教学探究中的重要任务。
如何发展学生的理性思维呢?——在探究中发展理性思维
一、教师创设条件引导学生探究,发展理性思维
探究学习中教师要改变角色,由主导者变成引导者,着重培养学生的理性思维能力 探究学习是深入探讨,演绎推理,进行理性思维的一种学习方式。在探究学习中怎样才能培养提高学生的理性思维能力呢?
1、夯实基础,打造探究学习平台
教学中经常听到有些老师埋怨:“这么简单的填空题,选择题老是错。”大部分学生也把错误简单归结为‘粗心’。其实‘罪魁祸首’是老师自己在教学过程中忽视数学概念,定理公式,运算法则等基本知识的教授,简单地把知识‘告知’学生,很快进入大量习题训练,造成学生概念不清,以至于后来反复纠正,还是没啥效果。究其原因,基础不扎实。因此在进行教学时,应遵循学生的认知规律,不仅要让学生知道“是什么”,还要激发学生探索“为什么”“换成其他方法行不行”等。这样既能使学生正确理解,掌握知识,还能激发学生的学习兴趣,培养学生优良的思维品质。例如:在讲“实数”时,一定要讲清实数的发展史,使学生理解概念的来龙去脉,加深对概念的理解,培养学生数学思维的严谨性。又如讲“多边形的内角和”,我是这样处理的:请同学们探索过n边形的一个顶点能作多少条对角线;接着问受此图形的启发你能计算n边形的内角和吗?谁还能给我们发明一种计算n边形的内角和的方法?学生很兴奋地以“发明家”的角色投入到对知识的探索中去。
2、创设情景 ,激发学生进行探究。
初中生年龄尚小,少有主动性较强的学生,因此,在教学中应创设具体、生动的情境,才能激发学生的学习兴趣,促使他们以积极的态度,饱满的热情和旺盛的精力主动地学习,从而获得最佳的教学效果。
例如:数轴概念的教学.,观察生活中的温度计的特点。进一步引导学生抽象出本质属性,用直线上的点表示数,从而引进 “数轴”的概念.这样做符合学生的认识规律,给学生留下深刻持久的印象,使学生认为自己创造了“数轴”,内心充满成就感。同时激发学生的学习兴趣,积极参与教学活动,有利于学生思维能力的培养。
3、设疑激趣。保护学生进行探究
兴趣是学生学习的动力源泉,是思维的激发点。教学中教师要千方百计提高学生的学习兴趣,让学生对知识充满好奇,对一切都有无穷的新鲜感。从而激发学生的探究热情,使学生满怀激情的投入到探究学习中。
孔子曰:疑,思之始,学之始。通过设疑能使学生产生认知学习的新鲜感,从而诱发学生的学习兴趣。如:在讲“一元二次方程根与系数的关系”一节时,复习完一元二次方程的解法后,我就满怀信心地说:“你们任给一个一元二次方程,我可马上说出它的两根之和,两根之积。”由学生任意举例,老师一口说出它的两根之和与积。再由学生自己求解验证为真,引发学生的好奇:那么快!老师用的是何妙法?我能吗?这样便能紧紧地抓住学生的心,激活学生的思维状态,学习兴趣油然而生。
4、设置障碍,激励学生进行探究
由于学生在探究中可能遇到障碍,使探究无法进行下去。这时,教师要及时引导,使学生的探究流畅,让学生及时得到成就感。从而培养学生思维的深刻性,以更大的热情投入到下一轮探究中去。
例如,如图,在三角形ABC中,AD⊥BC,AE平分∠BAC,试探究∠DAE与∠B,∠C之间的数量关系?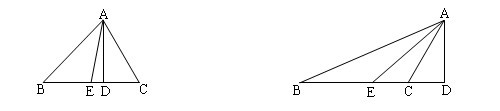
∠DAE与∠B,∠C之间的数量关系不明确,同学门对这种题型很少接触,一下子懵了。这反而激起学生的求知欲,但又不知如何下手。真是骑虎难下,欲罢不能。此时我适时给出∠B,∠C具体的度数,求∠DAE的大小,这并不很难,大部分同学很快给出解题方法及答案。我又重新给出一组数据,求∠DAE。通过具体角度的计算,大部分同学在解题过程中找到了解决问题的方法——只要把∠B,∠C代入计算过程即可。紧接我又提出一个问题:“上述条件不变,只是其中∠C是一个钝角,∠DAE与∠B,∠C之间的数量关系还成立吗?”学生马上回答:“成立!”“为什么!”同学们立马信心满满地拿起笔演算起来。由于图形的变化,同学们还是花了一定的时间才解决问题。在这一教学过程中,学生在掌握解题思想的基础上,也记住了结论。作到了探究,拓展,提高,总结,提升了理性思维。
5、恰当引导,促进学生进行探究。
由于学生知识的局限,在探究中可能会误入歧途。这时,教师要及时引导,使学生的探究走上正确的轨道,让学生的探究及时得到纠正,从而加深对正确思维方式的认识,培养自身理性思维的发展。
例如:如图,在直角三角形ABC中,∠C=90°,AD=AC,BE=BC, 求∠DCE的大小。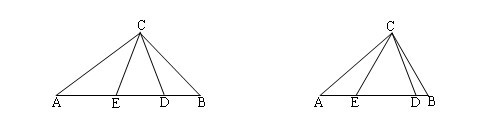
通过计算,不难求出∠DCE=45°。稍加引导,学生便轻易得出这样的结论:∠DCE=1∕2∠C.表面看起来,这个结论是正确的,没什么问题。不要说是学生会犯这样的错误,就连部分老师在给学生上课时,也是这样总结的。于是我反问:“真是这样的结论吗?”同学们各个用半信半疑而又渴求的眼神看着我。我又出一例:如图,在三角形ABC中,∠C=80°,AD=AC°BE=BC, 求∠DCE的大小。“∠DCE=40°吗?大家算算看!”为了验证自己的结论,同学们迫不及待拿起笔来。通过计算,得出∠DCE=50°。同学们议论纷纷:“咦!怪了!这是怎么回事呢?”我又不失时机地加以引导:“请同学们仔细回顾一下自己的计算过程,我相信你们会有新发现的!”于是同学们都很认真地研究自己的计算过程,终于发现:∠DCE=1∕2(∠A+∠B)。回到上例,嗷!正确的结论应该是这样的!
二、适当放手,培养学生自主探究学习习惯
人的潜能是无限的,千万不要忽视学生的能力,总认为学生这也不行那也不行,要相信他们可是一群给点“阳光”,就能“灿烂”的精灵。例如,在学习《测量》一节内容时,有的老师不知道要教给学生什么,有的老师干脆直接跳过。看似他们跳过的只是一节内容,却错过一次绝佳的培养学生自主探究学习的机会。我在课堂上充分让学生开动脑筋,想出尽可能多的,测量河的宽度,旗杆高度的方法,在这一教学活动中,学生不知不觉就把测量的方法总结了。最后,又给学生提了一个问题:测量旗杆时可以到达旗杆底部,如果要测量一座山的高度,而山的底部是达不到的,你如何能完成这个任务呢?一石激起千层浪,激起了学生兴趣,也激发了学生的思维。理性思维的培养不是一蹴而就的,要经历一次次的磨练才能逐渐得到发展,因此,培养学生自主探究学习习惯尤为重要。
数学的性质决定了数学教学既要以学生思维的深刻性为基础,又要培养学生的思维深刻性。学生要通过数学学习学会思维。教师利用课堂培养学生的理性思维是必要的,而且要不断改进方式、方法,力求取得更好的效果。简单说来,培养学生的理性思维,教师应当为之不懈努力!
